Skip to main content

Control Theory

The Goal of control theory is to pick control actions in an optimum manner without delay or overshoot and ensuring control stability [1]

PID - Control​

Example: Controlling a car to drive along x-axis

P ... Proportional

control_action = -Kp * error

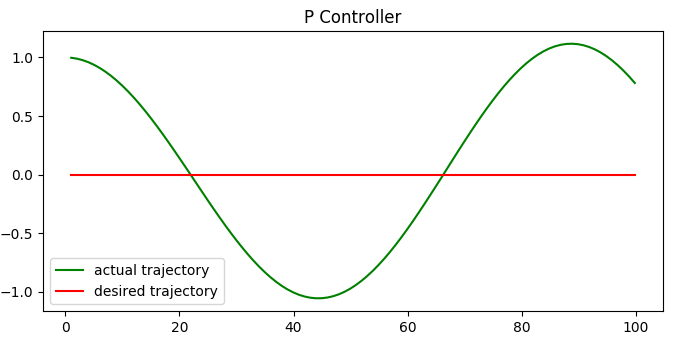
  • Problem: Overshoot
  • Solution: Add differential

D ... Differential

control_action = -Kp * error - Kd * diff_error

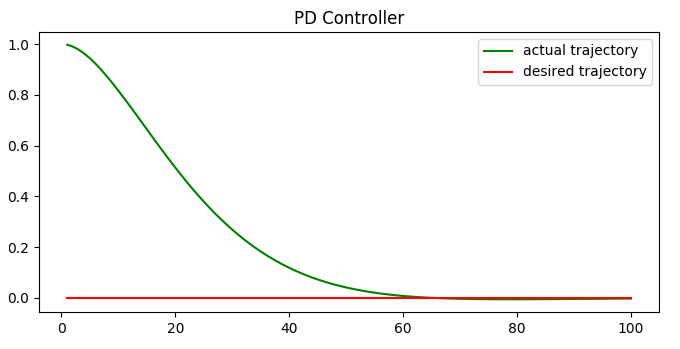
pd_controller

  • Another problem: system bias. Example: Car wheels are off-center
  • Solution: Add an Integral Part

I ... Integral

control_action = -Kp * error - Kd * diff_error - Ki * sum_error

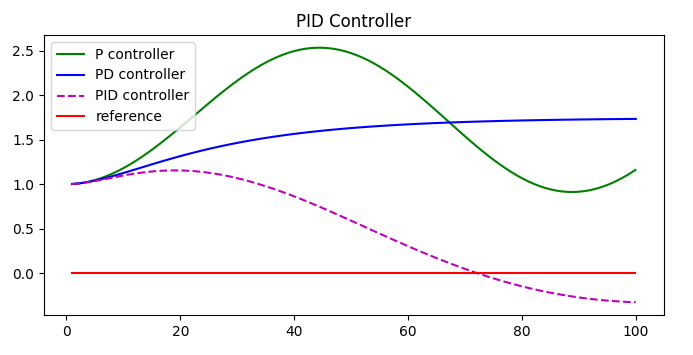
pid_controller

Source Code

prev_error = robot.y
sum_error = 0
dt = 1.0

# Simulation loop
for i in range(n):
    error = robot.y
    diff_error = (error - prev_error) / dt
    sum_error += error
    steer = -Kp * error - Kd * diff_error - Ki * sum_error
    robot.move(steer, speed)

Finding good PID parameter values​

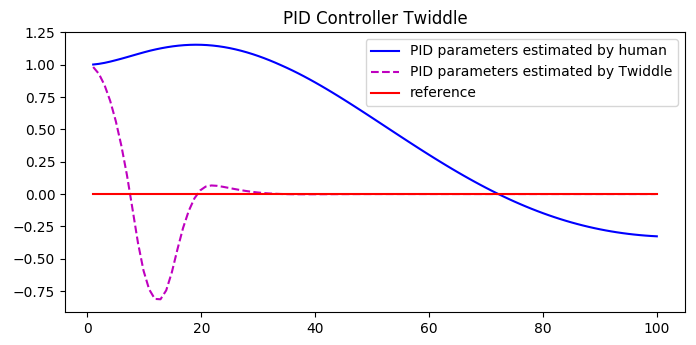
Step 1: Have a cost function which tells how "good" the PID parameters are. For instance the mean cross track error over some simulation period can be used.

def cost_func(robot, params, n=100, speed=1.0):
    prev_error = robot.y
    sum_error = 0
    mean_error = 0

    # Give the algorithm a chance to converge to 0 in n steps
    # Only from then on calculate the mean error
    for i in range(2*n):
        error = robot.y
        sum_error += error
        diff_error = (error - prev_error) / speed
        steer = -params[0] * error - params[1] * diff_error - params[2] * sum_error
        robot.move(steer, speed)
        prev_error = error
        if i >= n:
            mean_error += error ** 2
    return mean_error / n

Step 2: Implement the twiddle algorithm. The basic idea is to iterate over the parameters and then try out a value for the paramter which is dp above the parameter and dp below. If the change in value gives lowest cost so far then this parameter value is kept and dp is increased otherwise dp is decreased.

def twiddle(tol=0.2): 
    p = [0, 0, 0]
    dp = [1, 1, 1]
    robot = make_robot()
    x_trajectory, y_trajectory, best_err = run2(robot, p)

    it = 0
    while sum(dp) > tol:
        print("Iteration {}, best error = {}".format(it, best_err))
        for i in range(len(p)):
            p[i] += dp[i]
            robot = make_robot()
            err = cost_func(robot, p)

            if err < best_err:
                best_err = err
                dp[i] *= 1.1
            else:
                p[i] -= 2 * dp[i]
                robot = make_robot()
                err = cost_func(robot, p)

                if err < best_err:
                    best_err = err
                    dp[i] *= 1.1
                else:
                    p[i] += dp[i]
                    dp[i] *= 0.9
        it += 1
    return p

Step 3: Run twiddle:

Kp, Kd, Ki = twiddle()

Source​